Lesson Notes By Weeks and Term - Senior Secondary School 2

SUBJECT: PHYSICS

CLASS:  SS 2

DATE:

TERM: 1st TERM

REFERENCE TEXT

• New School Physics by M.W Anyakoha
• SSCE WAEC Past Questions
• UTME Past Questions

 
WEEK ONE

TOPIC: POSITION,DISTANCE AND DISPLACEMENT

CONTENT

• Position
• Coordinates System
• Distance
• Displacement

POSITION

The position of an object in space or on a plane is the point at which the object can be located with reference to a given point (the origin).          

COORDINATES SYSTEM

1. RECTANGULAR CARTESIAN COORDINATE SYSTEM

This is a system that consists of two or three intersecting lines mutually perpendicular and which serves as a reference frame that guides one in locating the position of a point in a plane or in space.

This system also assigns direction(with arrow head) to these reference lines(called the coordinate axes) and make the distances measured from the point of intersection(known as the origin)positive along OX, OY and OZ and that measured on the opposite direction, negative.

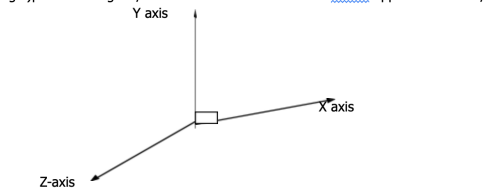
3:Dimensional coordinate system diagram.

PLANE

A plane is a geometric figure defined by two reference frame or 2-dimensional coordinate system.

SPACE

A space is  defined by three reference frames or 3-dimensional coordinate system.

EVALUATION

1.  With the aid of a diagram, explain the term “plane” and “space”.
2. Briefly describe how the position of a point can be located in space using rectangular Cartesian coordinate system

DISTANCE

This is a measure of the separation between two points. It has magnitude but no direction.Hence, it is a scalar quantity

DETERMINATION OF DISTANCE BETWEEN TWO POINTS

If two points A  and B located in a plane  are defined by two ordered  pair of values(x1 y1) and (x2 y2) or assumed to  be in space where they are defined by (x1 y1 z1) and (X2,  Y2 Z2)  the distance between them can be determined by applying the relation.

AB = [ ( x2 – x1)2 + ( y2- y1)2 ]1/2

EVALUATION

1. Calculate  the distance between points A(2,3) and B(-5,1).
2. Calculate the distance between points J(-2,-4) and K(-5,-10) in space.

DISPLACEMENT

Displacement is the distance covered in a specified direction. It is a vector quantity, that has the same unit as distance.

EVALUATION

1.  Why is displacement regarded as vector quantity?.
2. Differentiate between distance and displacement.

READING ASSIGNMENT

New School Physics for S S S-M W ANYAKOHA.Pages 121-126.

GENERAL EVALUATION

1. State 7 fundamental quantities.

2.for the fundamental quantities stated above give their respective units.

WEEKEND ASSIGNMENT

1. In the diagram below, the position of A is

4                (A)

2

0        1       2          3

(A)2,3   (B)3,3  (c)3,4   (D)4,3.

2, To locate a point in a plane or space, we can use.

(A)Bearing system.  (B) Centrifugal (C) Centripetal. (D) None of the above

3.Displacement can be classified as

(A) Scalar quantity (B)Vector quantity (C)Both scalar and vector quantities. (D)All of the above.

4. Determine the distance between S(3,4,-5)and T(2,1,0). (A)5.8  (B) 5.9  (C) 6.0  (D) 6.2.
5. Distance can be measured by.

(A) Tape rule (B) Eureka can (C) Lever balance. (D) Stop watch.

THEORY

1. Sketch clearly using scale indicators, the position of a point P (4,-5) and Q( -4, 10)with reference to a point Q(O,0). Determine the distance   between P and Q.
2. Distinguish between distance and displacement. Which of the terms is a vector and why?