WEEK 4
SUBJECT: MATHEMATICS
CLASS: PRIMARY 4
TERM: 3RD TERM
TOPIC: Angles
SUBTOPIC: properties of a square and rectangle
BEHAVIOURAL OBJECTIVES: At the end of the lesson, pupils should be able to:
- State the properties of a square
- State the properties of a rectangle
- Find the area of a rectangle using the formula
- Calculate areas involving square meters and hectares.
- Develop interest in finding shapes in their environment.
CONTENT
Properties of a square
- The diagonals of a square bisect each other and meet at 90°
- The diagonals of a square bisect its angles.
- Opposite sides of a square are both parallel and equal in length.
- All four angles of a square are equal. ...
- All four sides of a square are equal.
- The diagonals of a square are equal.
Properties of a rectangle
1.Opposite sides are equal.
2.All angles in a rectangle is 90 degrees.
3.Diagonals are equal and they bisect each other.They are also congruent.
4.Perimeter of a rectangle is 2(l+b) where l is length and b is breadth.
5.Area of rectangle is l*b.
6.Square of length of diagonal is the sum of squares of length and breadth.
AREA OF RECTANGLE AND SQUARE
To find the area by counting sguares could take a long time especially if you have to find the area of a large surface There is a formula to calculate the area of a rectangle or a square.
Example:
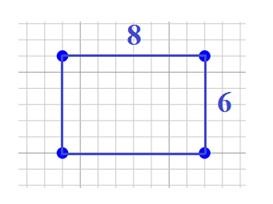
The formulary for calculating the area of a rectangle is A = L×B
Lenght = 8cm
Breadth= 6cm
Area= 8cm×6cm
= 48cm²
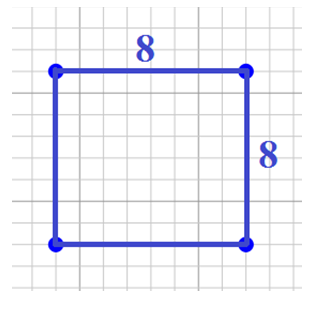
A= L× L
L= 8cm
B= 8cm
A= 8cm×8cm
A= 64cm2

Length= 3ft
Breadth=5ft
Area: L xB
A= 3 x 5ft.
A= 15ft.
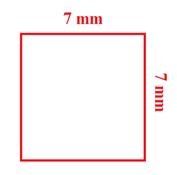
Length= 7mm
Breadth=7mm
Area= LxB
A= 7mm x7mm
A=49mm.
Class work
Calculate the area of the following:
- Rectangle 9cm by 3cm. 2. Rectangle 4cm by 7cm. 3. Rectangle 10cm by 2cm
- Rectangle 9cm by 1cm. 5. Rectangle 2cm by 5cm. 6. Rectangle 9cm by 2cm
- Calculate the area of the following:
- Square side 5cm. 2. Square side 3cm. 3. Square side 6cm. 4. Square side 4cm.
- Square side 8cm. 6. Square side 7cm
Examples
ding either the length or breadth of a rectangle, you simply divide the given area by
either the breadth or the length.
4 cm
Area = 12 cm2
Area = 12 cm2 Length = 4 cm
$ Breadth = 12/4
= 3 cm
Area = 21 cm2 3 cm
Area = 21 cm2 Breadth = 3 cm
$ Length = 21/3
= 7 cm
Exercise 3
Calculate the length or breadth required for each of the following rectangle where the units
for length and breadth are in centimetres.
- Area = 48, Length = 6 2. Area = 12, Breadth = 2 3. Area = 36, Breadth = 6
- Area = 20, Breadth = 4 5. Area = 100, Length = 10 6. Area = 11, Breadth 7. Area = 120, Length = 10 8. Area = 21, Length 4 9. Area = 72, Length 12
- Area = 80, Breadth 8
To find the side of a square when only the area is given, simply work out the square
root of the area.
Side of a square = Area
Exercise 4
Calculate the sides of each of the squares.
- Area = 100 cm2 2. Area = 49 cm2 3. Area = 64 cm2 4. Area = 144 cm2
- Area = 36 m2 6. Area = 81 m2 7. Area = 25 m2 8. Area = 16 m2
- Area = 169 m2 10. Area = 4 cm2
SQUARE OF A METER AND HECTARE
The square metre is too small to measure very large areas such as states, countries, etc.
The area of Nigeria in square metres is 923 768 000 000 m2
The number of digits are reduced when we use acre and it is reduced further when
we use hectare.
The acre is 4 000 m2 and it is more convenient for measuring fields but the most
common units are the hectare and square kilometre.
1 acre = 4 000 m2 1 hectare = 2 1/2acres = 10 000 m2
1 square kilometre = 1 000 000 m2 = 100 hectares
Exercise 1
- Write down the area of Nigeria in
- acres 2. hectares 3. square kilometres
Convert these to acres.
- 7 hectares 5. 18 hectares 6. 53 hectares
- 9.6 hectares 8. 14 hectares 9. 30.7 hectares
- 82.1 hectares 11. 14.27 hectares 12. 35.84 hectares
- Convert these to acres.
- 12 000 m2 2. 8 000 m2 3. 16 000 m2 4. 24 000 m2 5. 36 000 m2 6. 60 000 m2 7. 14 000 m2 8. 10 000 m2 9. 6 000 m2 10. 7 500 m2
Remember 1 acre = 4 000 m2
Exercise 2
Convert these to hectares. Remember 1 hectare is 2 12
acres.
- 600 acres 2. 200 acres 3. 450 acres 4. 129 acre 5. 285 acres 6. 2 036 acres 7. 1 963.2 acres 8. 3 001.8 acres 9. 20 000 m2 10. 80 000 m2 11. 36 000 m2 12. 49 000 m2 13. 24 600 m2 14. 51 200 m2 15. 17 650 m2 16. 90 160 m2 17. 74 380 m2 18. 66 210 m2
Exercise 3
- Find the breadth of one hectare of farmland with
- a) Length – 500 m b) Length – 1 000 m
- Find the length of one acre of a poultry farm with
- a) Breadth – 400 m b) Breadth – 200 m
- A land speculator bought 10 hectares of land and mapped out 200 plots for sale. What
was the area of each plot?
- Calculate the area of 10 of the plots in question 3
- The area of the Federal Capital Territory, Abuja is about 925 000 km2. Convert this to metre2.
Exercise 4
Word problems
- The area of a town is 14 400 square metres. Find the width if the length is 300 metres.
- Find the area of a rectangle 24 cm long and 9 cm wide.
- A tray is 18 cm wide and 28 cm long. What is the area of the surface of the tray?
- Kitchen tiles are 30 by 20 cm. What is the area of each tile.
- How many kitchen tiles are needed to cover one side of my kitchen wall measuring
300 cm by 200 cm.
- A floor is rectangular in shape and it measures 4.5 m by 4 m. What is the area?
- A rectangle has length 25 cm and breadth 18 cm. If a diagonal is drawn to form
two triangles, find the area of one triangle.
- How many squares of 2 cm side can be cut from a square 10 cm side.
- Find the area of a plot of land 40 m long and 18 m wide.
- An oil company is drilling oil in a rectangular plot measuring 28 kilometres by
37 kilometres. What is the area of the plot? Answer in km2.



