TERM: 2nd TERM
SUBJECT: BASIC TECHNOLOGY
CLASS: JSS 2
REFERENCE MATERIALS
- MELROSE, Basic Science and Technology, Book 2
- NERDC, Basic Technology for JSS, Book 2
WEEK FOUR AND FIVE
TOPIC: AREA OF PLANE FIGURE
INTTRODUCTION
Plane figures are flat two-dimensional shapes. The can be made of straight lines, curved lines or both straight and curved lines. Examples of plane figures are: triangle, square, parallelogram, circle, rectangle etc.
AREA OF PLANE FIGURES
When a plane figure is drawn, it occupies a certain amount of space. At times, it is important to know the amount of space of a figure occupies, when it is drawn. This way, it will be possible to draw a different shape that has the same amount of space with it.
Therefore, area of a plane figure can be defined as the space it occupies.
Area of a triangle

Area = ½ of (b x h) where b=base and h= vertical height
Note: The area of any plane figure (polygon) can be reduced to a combination of areas of rectangles (Or squares) and triangles each of which can be computed and the total area together.
Area of a rectangle
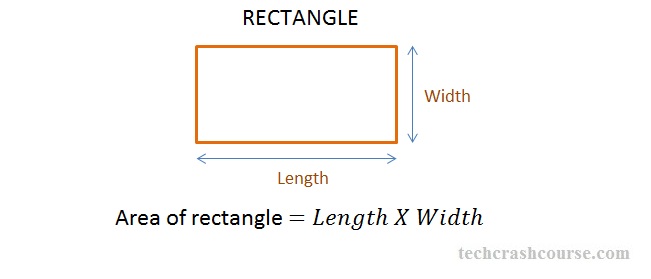
Area= l x b where l= length and b= breadth
Area of a square
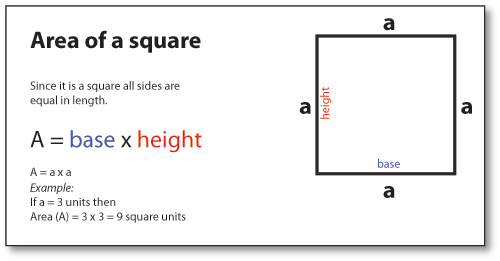
Area= a x a= a2 where a= length of side
Area of a parallelogram

Area= b x h where b= base and h= vertical height
Area of a circle
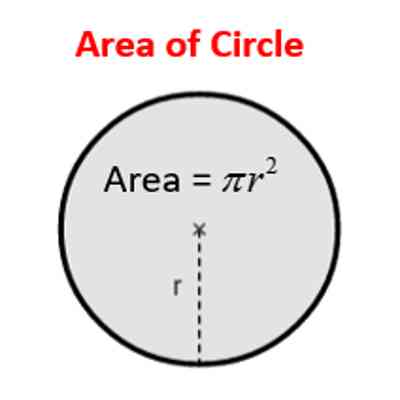
Area= πr2 where r= radius
Evaluation
- Define the area of plane shape.
- State the area of (i) triangle (ii) rectangle
THEOREMS
In construction regular plane figure of equal areas, some geometrical laws, generally called theorems, are applied. For instance, the following are will be relevant to this topic:
- Triangles on the same base and between the same parallels are equal in area.
- Triangles on equal bases and between the same parallels are equal in area.
- Parallelograms on the same base and between the same parallels are equal in area.
- Parallelograms on equal base and between the same parallel are equal in area.
- A triangle on the same parallels with a parallelogram is half the area of the parallelogram.
- If a triangle and a parallelogram are on equal bases and between the same parallels, the triangle is half the area of the parallelogram
Evaluation
- State 6 theorems of area of plane shape
- Sketch diagrams that demonstrate the theorems of plane shape.
CONSTRUCTION OF SIMILAR AREA OF PLANE SHAPES
Constructing a triangle equal in area to a given rectangle
Procedure
- Draw the rectangle ABCD
- Project line CD and mark off DE, using the distance equal to CD.
- Draw a horizontal line from point F to line BA parallel to BC.
- Locate point G anywhere on line EF.
- Join point G to B and C respectively, to obtain the triangle equal in area to rectangle ABCD. Triangle BCG is equal to the given rectangle.
Constructing a rectangle equal in area to a given triangle
Procedure
- Draw the given triangle ABC.
- Draw a line through A, parallel to BC.
- Bisect line BC perpendicular at D and to meet the line through at D and to meet the line through A at E.
- Draw a perpendicular to BC at B meet the line through A at F.
- FBDE is the rectangle required
Evaluation
- Construct a triangle equal in area to a rectangle AB=50mm, BC=60mm.
- Construct a rectangle equal in area to a triangle ABC, AB= 40mm, AC=70mm and BC=60mm
Constructing a triangle equal in area to any regular polygon
Procedure
- Draw the regular polygon (hexagon) ABCDEFG
- Draw the diagonals to intersect at the centre of the polygon O.
- Draw HI equal in length to the length of side x number of sides. In this exercise, GH is equal to six times, the length of the side of the hexagon. (HI= 6 x y mm)
- Join O to G and H, GOH is required triangle
Constructing a triangle equal in area to a given circle
Procedure
- Draw the given circle of diameter AB and centre O.
- Divide the radius OA into 7 equal parts
- Draw a perpendicular line at A equal in length to 3 1/7
- Join C to B.ACB is the required triangle
Reducing an irregular quadrilateral to half its original area
Procedure
- Draw the given irregular quadrilateral ABCD
- Draw a diagonal BD
- Bisect AB perpendicular at E
- With centre E and radius EA, draw an arc to meet the bisector at F.
- With centre B and radius BF, draw an arc, which meets the bisector at F.
- From G and GH parallel to AD, also draw HI parallel to DC.
- GBIH is required reduced irregular quadrilateral.
Evaluation
- Construct a triangle equal in area to any regular hexagon 50mm.
- Draw a triangle equal in area to a given circle of radius 40mm.
READING ASSIGNMENT
Read more about AREA OF PLANE FIGURES
REFERENCE MATERIALS
- MELROSE BASIC SCIENCEBASIC TECHNOLOGY BOOK 2, page 86-92
- NERDC- BASIC TECHNOLOGY BOOK 2, page 61-63
WEEKEND ASSIGNMENT
- The space which a plane shape occupies is known as _______ A. triangle B. rectangle C. parallelogram D. area
- The units of area are as follows except A. mm2 B. cm2 C. kg2 D. m2
- Triangles on the same base and between the same parallels are equal in area A. True B. False C. None of the above D. All of the above
- A triangle on the same base and between the same parallels with a parallelogram. A. True B. False C. None of the above D. All of the above
- The area of a triangle is ____A. ½ B x H B. B x H C. B2 x H D. B x H2
THEORY
- State 6 theorems of area of plane shape
- Construct a right-angled triangle, which has the same area with an equilateral triangle of side 60mm.




